 共31章节566课时
共31章节566课时
【全科班】汇川中型PLC从0到1就业班(Codesys系统化全科班课程-600节+)-汇川PLC教程
朱子文
 共30章节583课时
共30章节583课时
【全科班】汇川技术H5U从0到1就业班(系统化全科班-600节+)
张汉清
 共9章节44课时
共9章节44课时
【09-Codesys教程】电子凸轮齿轮从入门到进阶系统化课程-色标跟踪-探针-追剪-飞剪-间歇式工艺-汇川中大型PLC伺服多轴同步运控
朱子文
 共5章节63课时
共5章节63课时
【01-Codesys教程】ST文本从0到1,从入门到进阶-汇川中大型PLC教程
朱子文
 共6章节52课时
共6章节52课时
【10-Codesys】包装行业-三伺服枕包机实战项目(4虚轴3实轴耦合+凸轮动态修改+防切工艺+防空工艺+色标探针+挺杆功能+状态机编程+程序框架+指针FIFO)
朱子文
探究动力学模型的应用以及特点 |
| |
相关帖子
|
|
| |
| |
 共31章节566课时
共31章节566课时
【全科班】汇川中型PLC从0到1就业班(Codesys系统化全科班课程-600节+)-汇川PLC教程
朱子文
 共9章节44课时
共9章节44课时
【09-Codesys教程】电子凸轮齿轮从入门到进阶系统化课程-色标跟踪-探针-追剪-飞剪-间歇式工艺-汇川中大型PLC伺服多轴同步运控
朱子文
 共30章节583课时
共30章节583课时
【全科班】汇川技术H5U从0到1就业班(系统化全科班-600节+)
张汉清
 共5章节63课时
共5章节63课时
【01-Codesys教程】ST文本从0到1,从入门到进阶-汇川中大型PLC教程
朱子文
 共6章节52课时
共6章节52课时
【10-Codesys】包装行业-三伺服枕包机实战项目(4虚轴3实轴耦合+凸轮动态修改+防切工艺+防空工艺+色标探针+挺杆功能+状态机编程+程序框架+指针FIFO)
朱子文
 共4章节36课时
共4章节36课时
03 中大型ST文本结合仿真软件小项目 31节-气缸功能块封装-状态机编程思路-小设备框架
朱子文
 共4章节29课时
共4章节29课时
【12-Codesys小课】中大型PLC-PID控制器算法从入门到进阶之液位控制系统
朱子文
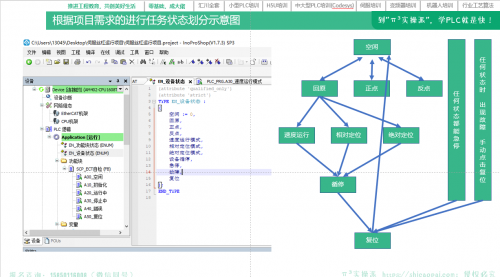 共3章节30课时
共3章节30课时
【05-Codesys教程】汇川中大型PLC单轴运动控制教程-汇川PLC教程
朱子文
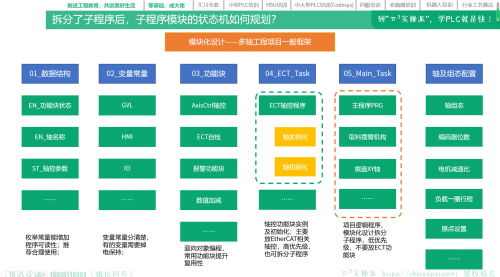 共3章节25课时
共3章节25课时
【06-Codesys教程】汇川中大型PLC运动控制进阶篇(多轴PTP)-编程框架与编程模板实操
朱子文
 共3章节24课时
共3章节24课时
【08-codesys教程】汇川中大型codesys教程-多轴运控扩展篇经验分享小知识分享
朱子文
 共31章节566课时
共31章节566课时
【全科班】汇川中型PLC从0到1就业班(Codesys系统化全科班课程-600节+)-汇川PLC教程
朱子文
 共9章节44课时
共9章节44课时
【09-Codesys教程】电子凸轮齿轮从入门到进阶系统化课程-色标跟踪-探针-追剪-飞剪-间歇式工艺-汇川中大型PLC伺服多轴同步运控
朱子文
 共30章节583课时
共30章节583课时
【全科班】汇川技术H5U从0到1就业班(系统化全科班-600节+)
张汉清
 共5章节63课时
共5章节63课时
【01-Codesys教程】ST文本从0到1,从入门到进阶-汇川中大型PLC教程
朱子文
 共6章节52课时
共6章节52课时
【10-Codesys】包装行业-三伺服枕包机实战项目(4虚轴3实轴耦合+凸轮动态修改+防切工艺+防空工艺+色标探针+挺杆功能+状态机编程+程序框架+指针FIFO)
朱子文
 共4章节36课时
共4章节36课时
03 中大型ST文本结合仿真软件小项目 31节-气缸功能块封装-状态机编程思路-小设备框架
朱子文
 共4章节29课时
共4章节29课时
【12-Codesys小课】中大型PLC-PID控制器算法从入门到进阶之液位控制系统
朱子文
 共3章节30课时
共3章节30课时
【05-Codesys教程】汇川中大型PLC单轴运动控制教程-汇川PLC教程
朱子文
 共3章节25课时
共3章节25课时
【06-Codesys教程】汇川中大型PLC运动控制进阶篇(多轴PTP)-编程框架与编程模板实操
朱子文
 共3章节24课时
共3章节24课时
【08-codesys教程】汇川中大型codesys教程-多轴运控扩展篇经验分享小知识分享
朱子文
公司地址:江苏省苏州市吴中区越溪街道天鹅荡路5号31B13